Für kommenden Mittwoch ist zu einer SP-Sitzung geladen, auf der die Ausschüsse des Studierendenparlaments der Uni Bonn nach einem entsprechenden Ältestenratsbeschluss neu besetzt werden sollen; derweil streiten sich die Größen der Bonner Hochschulpolitik munter weiter bis in die nächste Instanz.
Doch ignorieren wir das alles mal und wenden uns der eigentlichen Frage zu: Wie problematisch ist das Rüngler-Problem?
Die Fakten
Das Studierendenparlament hat 43 Sitze. Die Ausschüsse des Studierendenparlaments werden auf Basis dieser Sitzverteilung besetzt, nach dem Sainte-Laguë/Schepers-Verfahren. Die Anzahl der Ausschussmitglieder ist zunächst einmal sinnigerweise ungerade. Die Satzung der Studierendenschaft sieht Ausschussgrößen von 3, 5, 7 und 9 vor. Eine SP-Mehrheit hat also mindestens 22 Sitze, eine Ausschussmehrheit entsprechend 2, 3, 4 oder 5.
Das Problem (Wiederholung)
In der aktuellen Besetzung hat das Studierendenparlament das Problem, dass die SP-Mehrheit von RCDS und Jusos mit 22 Sitzen in einem Fünferausschuss nur 2 Sitze besetzen kann, also keine Mehrheit in diesem Ausschuss hätte. Entsprechendes gilt für einen Neunerausschuss. Erklärbärartikel zum sog. “Rüngler-Problem”
Was tun?
Zunächst einmal wollen wir die Frage beantworten, mit welchen Wahlergebnissen wir eigentlich rechnen müssen. Da für unser Problem nicht die Identität der Listen, sondern nur das Verhältnis ihrer Sitzzahlen interessant ist, genügt es, die Sitzverteilungen absteigend sortiert zu berechnen. Ein kleines Python-Skript mit einer zehnfach verschachtelten For-Schleife erledigt dies für 2 bis 10 antretende Listen in erstaunlicherweise weniger als einer Sekunde1. Wen diese Ergebnisse interessieren: klick.
Doch damit beginnt der große Spaß ja erst. Nun wird jede dieser Sitzverteilungen darauf geprüft, für welche Ausschussgrößen das Rüngler-Problem auftritt. Alternativ kann natürlich auch das Sainte-Laguë/Schepers-Verfahren zu viele Sitze zuteilen, was ebenfalls nicht wünschenswert, aber hier nicht primärer Gegenstand unserer Betrachtung ist.
Resultate
Ei, ei, ei.
Nehmen wir mal an, der RCDS hätte einen Sitz weniger und die Piraten-Hochschulgruppe einen Sitz mehr im Studierendenparlament. Abstrakt sieht das ganze also so aus:
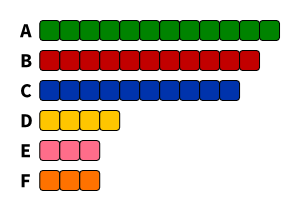
Unsere Beispielverteilung.
Nun bilden wir unsere Ausschüsse mit dem bewährten Sainte-Laguë/Schepers-Verfahren. In den folgenden Grafiken markiert die gestrichelte Linie die Mitte. Alle Listen links und auf dieser Linie besitzen zusammen eine Mehrheit im Ausschuss.
Dreierausschuss

B+C: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem
Fünferausschuss

A+D: Nur 16 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem
Siebenerausschuss

B+C: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem
Neunerausschuss

C+D+E+F: Nur 20 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem
Aber hey, es ist Karneval! Versuchen wir es doch mal mit einem Elferrat, dat hätt noch emmer joot jejange!
Elferausschuss (nicht satzungskonform)

B+D+E+F: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem
Wat fott es, es fott. *hust*
Herr Doktor, wie schlimm isset?
Schlimmstenfalls treten bei der nächsten Wahl 8 Listen an und es ergibt sich folgendes Ergebnis:
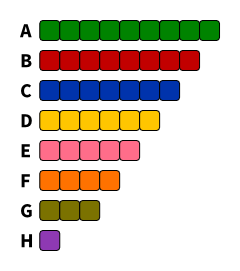
Können wir das machen? Bitte?
Dann haben wir das Rüngler-Problem bei einer Ausschussgröße von 3. Und bei 5. Und bei 7. Und 9. Und 11. Und 13. Überhaupt bei jeder ungeraden Zahl zwischen 2 und 42 – außer bei 23: Da schlägt dann das Sainte-Laguë/Schepers-Verfahren fehl, weil fünf Listen gleichzeitig die letzten vier Sitze zugeteilt bekämen. Die Rüngler-Lösung, bei der einfach die Ausschussgröße so weit nach oben korrigiert wird, bis das Problem nicht mehr auftritt, würde also zu 43er-Ausschüssen führen – da kann man dann eigentlich gleich eine SP-Sitzung einberufen.
Nun haben wir Extrembeispiele gesehen. Blicken wir nun auf einen Graphen, der die Wahrscheinlichkeit abbildet, dass bei einer der vier von der Satzung vorgesehenen Ausschussgrößen das Rüngler-Problem auftritt, oder das Sainte-Laguë/Schepers-Verfahren (STLGS) nicht die gewünschte Zahl an Sitzen zuteilen kann.
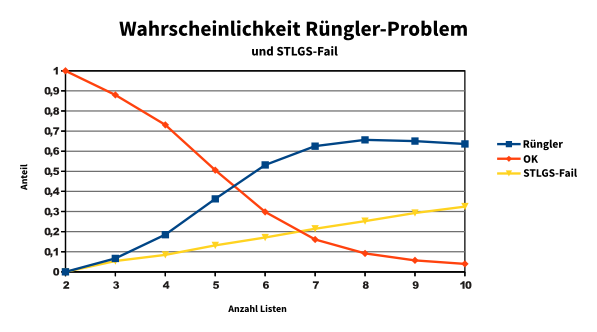
Aufgeteilt wird das ganze nach der Anzahl der im SP vertretenen Listen.
Wir sehen: Je mehr Listen im SP sitzen, desto wahrscheinlicher wird es, dass das Sainte-Laguë/Schepers-Verfahren für eine der Ausschussgrößen fehlschlägt, und noch stärker steigt die Wahrscheinlichkeit, dass das Rüngler-Problem auftritt.
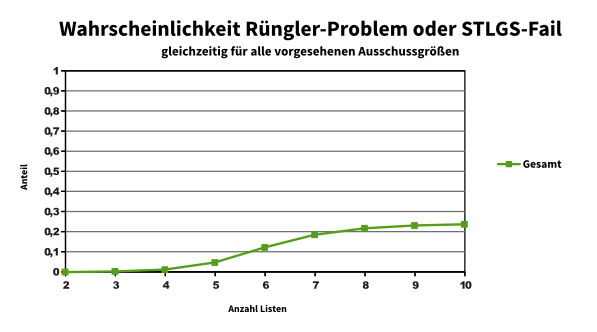
Eine Grafik hab ich noch: Wie wahrscheinlich ist es, dass für alle vier vorgesehenen Ausschussgrößen entweder das Rüngler-Problem auftritt oder das Sainte-Laguë/Schepers-Verfahren nicht die gewünschte Zahl an Sitzen zuteilen kann?
Sieht verschmerzbar aus. Wobei: 10 % sind eigentlich doch ganz schön viel. Anscheinend konvergiert das gegen 25 %, also jedes vierte Wahlergebnis wäre höchstproblematisch. Gegen zu viele Listen im SP könnte ja eine Sperrklausel bei der Wahl helfen *diabolisches Grinsen*
Fazit
Wenn das Rüngler-Problem ein Problem ist, ist es tatsächlich ein Problem.
So, für heute habe ich nun mit genug Zahlen und Bildern um mich geworfen. Das gesamte Team von hszemi.de wünscht allen Beteiligten viel Vergnügen bei der Lösung dieses Problems!
Disclaimer: Menschen machen Fehler. Falls ihr in den obigen Zahlen und Grafiken einen Fehler bemerkt, freue ich mich über einen Hinweis, zum Beispiel in den Kommentaren.
- Für eine einzige Liste ist dies trivial. Beweis durch scharfes Hinschauen. (Für 2 Listen eigentlich ja auch.) ↩