Wer Missetaten begehen will, überlegt sich oft zuerst, wie mit möglichst wenig Aufwand möglichst viel Unheil angerichtet werden kann. Da sprechen wir dann von Aufwand und Ertrag, oder dem allseits bekannten Kosten-Nutzen-Verhältnis.
Ein Beispiel: Nehmen wir einmal an, wir möchten die Wahlen zum Studierendenparlament trollen. Weit hergeholt, ich weiß.
Das teuerste an so einer Wahl ist die Bezahlung der Wahlhelfenden. Das zweitteuerste dürfte die Wahlzeitung sein.
In der Wahlzeitung bekommt jede Liste eine vorher festgelegte Anzahl an Seiten, auf denen sie ihr Wahlprogramm ausbreiten darf. Dafür sind ihr, abseits der allgemeinen Gesetzeslage, keine inhaltlichen Grenzen gesetzt.
Nun gibt es da einen interessanten Aspekt, der bislang wenig Beachtung gefunden hat. Für die Einreichung einer Liste benötigt man pro volle 1000 Wahlberechtigte eine Unterstützungsunterschrift. Aktuell sind das etwa 35 Unterschriften.
Bis 2014 galt: Jede Person darf nur eine einzige Listenbewerbung unterstützen.
4. je volle tausend Wahlberechtigte eine Unterstützer/innen/unterschrift. Kandidat/inn/en gelten als Unterstützer/innen. Jede/r Wahlberechtigte/r kann nur eine Wahlbewerbung unterstützen.
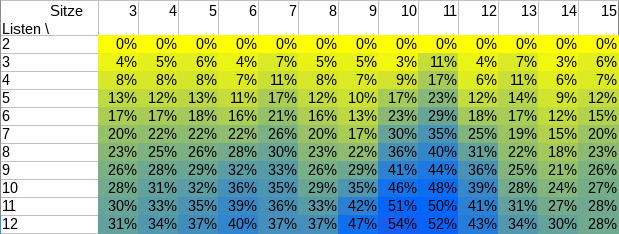
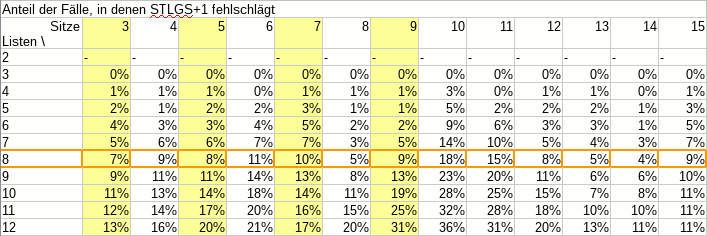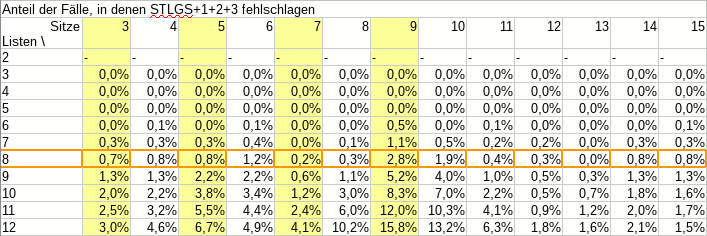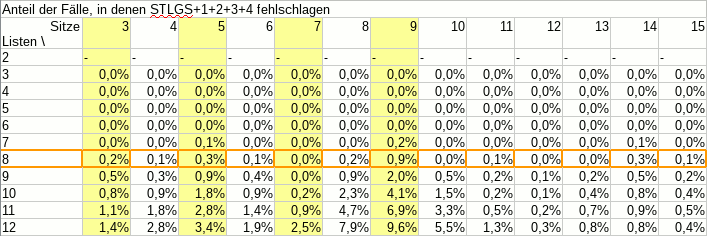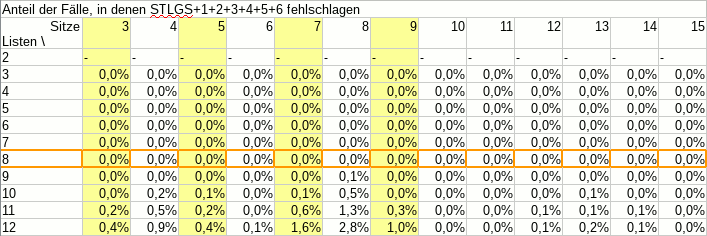
Man könnte auf die Idee kommen, eine oder mehrere Troll-Listen anmelden, um unter anderem die Wahlzeitung aufzublähen und Kosten zu verursachen. Wir nennen dieses Verfahren an dieser Stelle mal “Listenblähung”. Das Aufwand-und-Ertrag-Diagramm dafür sah bis 2014 folgendermaßen aus:
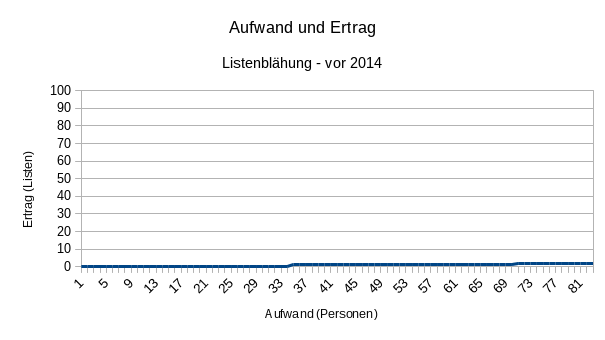
“Die Skalierung der Y-Achse ist aber misslungen”, mag hier die ein oder andere meinen. Tja…
Pro Trollliste wurden 35 Personen benötigt, die die Liste unterstützen, und von denen mindestens eine für die Liste kandidiert. Bei der aktuellen Hochschulpolitik-Unlust innerhalb der Studierendenschaft unwahrscheinlich, dass damit größerer Schaden angerichtet werden kann. Ein unattraktives Vorgehen! Dann klaut man doch lieber eine Wahlurne.
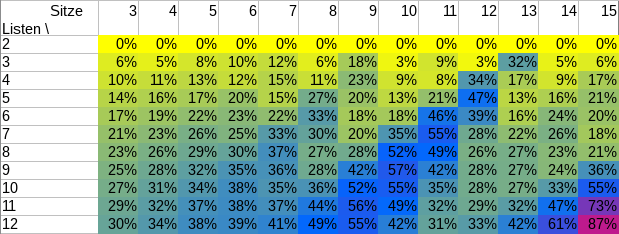
Mit der Reform der SP-Wahlordnung 2014 hat sich auch die Regel für Unterstützungsunterschriften geändert. Eine Person darf nun mehrere Listen unterstützen. Weil das dann weniger Probleme verursacht, war damals die Idee dahinter.
1. Je volle tausend Wahlberechtigte eine Unterstützungsunterschrift einer wahlberechtigten Person. Wer Teil einer Listenbewerbung ist, unterstützt diese gleichzeitig. Jede Person kann mehrere Listenbewerbungen unterstützen.
Was sagt unser Diagramm?
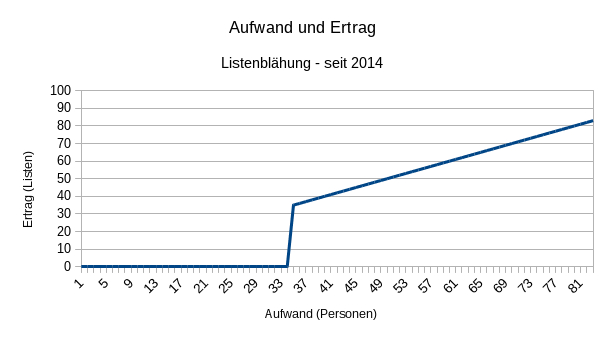
Äh. Ja, hoppla!
Sobald die magische Schwelle von 35 Personen1 überschritten ist, kann eine Liste pro Person eingereicht werden. (Zahlenmenschen sprechen von einer linearen Abhängigkeit.) In den letzten Jahren waren 4 DIN-A4-Seiten pro Liste Standard in der Wahlzeitung, damit wären wir bereits mit 35 zusätzlichen Listen bei 170+ Seiten. Das ist natürlich auch ein Weg, eine Dissertation zu veröffentlichen. Vom entstehenden Chaos auf dem Stimmzettel, der plötzlich 35 Einpersonenlisten zusätzlich aufnehmen muss, ganz zu schweigen.
Zusammenfassung
Sind sich >35 Studierende einig, dann können sie eine Studierendenparlamentswahl ganz legal hart sabotieren. Möglich machte das eine Wahlordnungsänderung 2014.
Wenn sich >2000 Studierende finden, die für eine Urabstimmung zum fzs-Austritt unterschreiben, dann finden sich bestimmt auch 40 Studierende, die Trolllisten unterstützen.
- Oder wo auch immer sie dann genau liegt, das schwankt ja. ↩