22. Januar 2017

Schäfer beißt Hund

Im Jahr 2013 wurde die Satzung der Studierendenschaft geändert. Damit einher ging ein Wechsel des Sitzzuteilungsverfahrens bei der Studierendenparlamentswahl. Wurde bis dahin das d’Hondt-Verfahren eingesetzt, so kommt seitdem das Wahlverfahren Sainte-Laguë/Schepers zum Einsatz.

Begründet wurde die Änderung damit, dass d’Hondt größere Listen bevorzuge, während Sainte-Laguë¹ dies nicht tue.

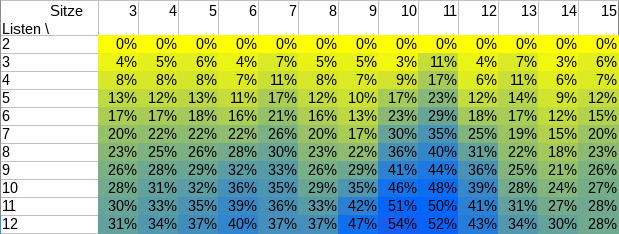
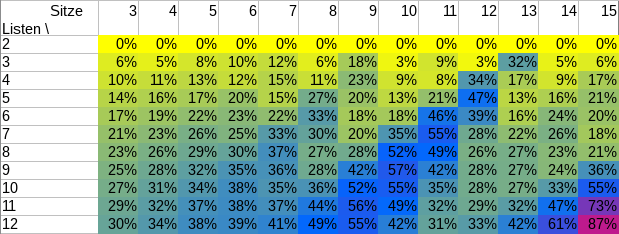
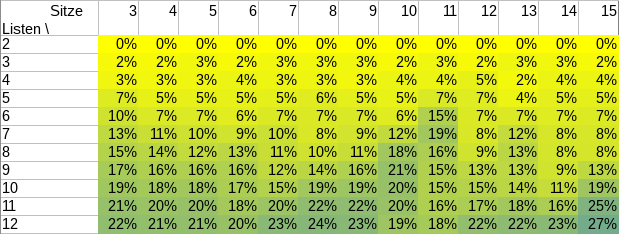
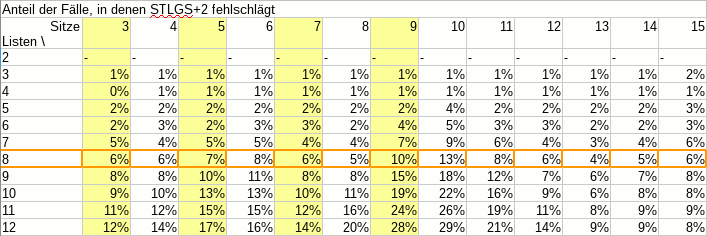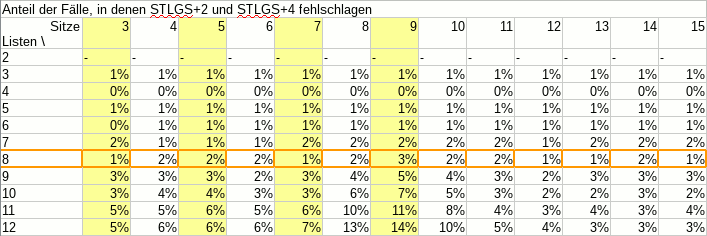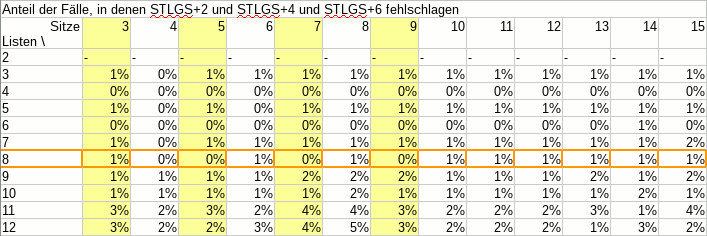
Gleichzeitig wurde das Verfahren für die Sitzzuteilung in den Ausschüssen des Studierendenparlaments ebenfalls zum Sainte-Laguë-Verfahren geändert. Was das konkret bedeutet, kann man am neuesten Wahlergebnis sehen:

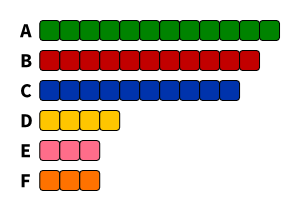
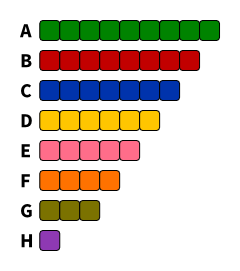
Liste	Sainte-Laguë	d’Hondt
RCDS	9	10
JUSOS	12	13
LHG	6	6
LUST	3	3
LISTE	2	1
KULT	3	2
GHGP	7	7
SDS	1	1

Die beiden größten Listen erhalten bei d’Hondt je einen Sitz mehr, den im Gegenzug kleinere Listen verlieren.

Schon im letzten Jahr hätte mit d’Hondt der RCDS einen Sitz mehr und KULT einen Sitz weniger errungen, und vor drei Jahren hätte die GHG einen Sitz von der LUST übernommen. Die jeweils größte Liste profitiert in diesen Fällen also stets vom d’Hondt-Verfahren.

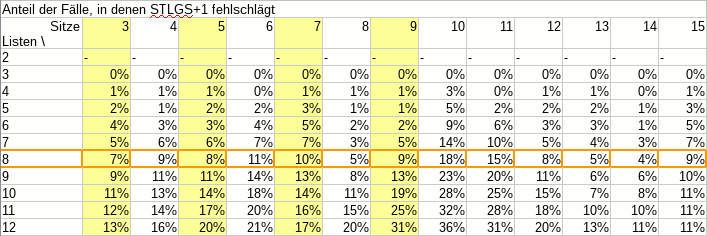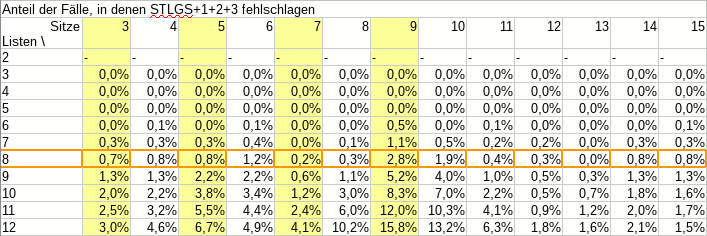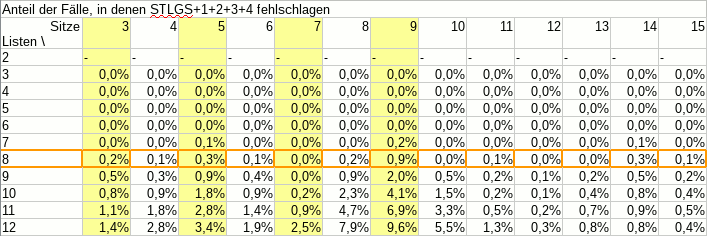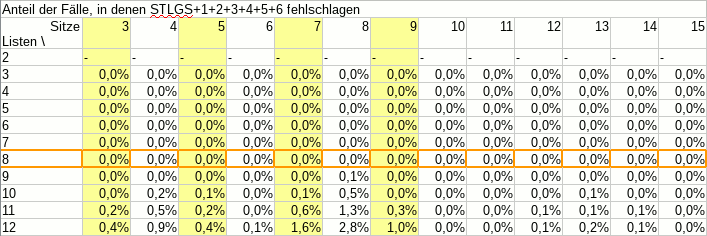
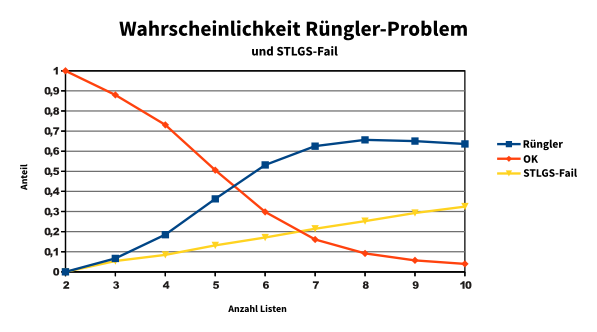
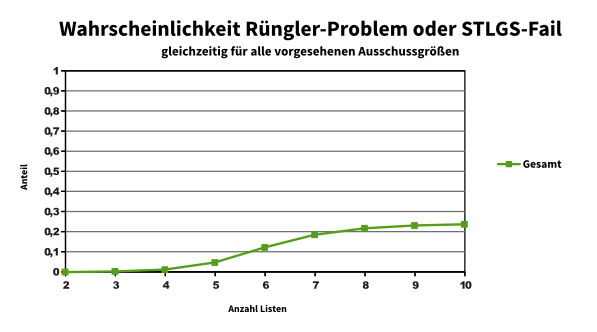
In other news: Der Sainte-Laguë/d’Hondt-Rechner kennt jetzt auch die Zahlen des Ergebnisses von 2017. Wir ~~rechnen ein wenig~~ lassen ein wenig rechnen und sehen: Bei der Besetzung der SP-Ausschüsse dürfen sich dieses Jahr für den Haushaltsausschuss der RCDS, die LUST und KULT um den letzten Platz kloppen.

Wäre doch voll kluk gewesen, wenn man da im letzten Jahr ein unblutiges Verfahren für festgelegt hätte…

Sprich: sɛ̃tlaˈɡy (“Sohnt’-Lagüüh”) ↩

10. April 2016

Die wunderbare Welt des Sainte-Laguë/Schepers-Verfahrens

Das Studierendenparlament hat seine Ausschüsse nach mittlerweile zwei Monaten immer noch nicht voll besetzt. Eins der Probleme¹ ist, dass das zur Sitzzuteilung verwendete Sainte-Laguë/Schepers-Verfahren nicht für jede SP-Besetzung eindeutige Ausschussbesetzungen erzeugen kann. Besonders häufig tritt das Problem auf, wenn Fraktionen im Parlament die selbe Sitzzahl haben und dann bei Zuteilung des letzten Sitzes gleichzeitig “an der Reihe” wären.

Oft wird und wurde vorgeschlagen, dann die Sitzzahl im Ausschuss einfach zu erhöhen. Wie erfolgsversprechend das ist, wollen wir heute betrachten.

Zunächst stellt sich die Frage, wie häufig das Problem überhaupt auftritt. Ich habe also die Wahrscheinlichkeit berechnet, dass das Sainte-Laguë/Schepers-Verfahren (im folgenden STLGS) fehlschlägt, und zwar für 2-12 vertretene Listen und Ausschussgrößen von 3 bis 15².

Wahrscheinlichkeit, dass STLGS fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)

Zum Vergleich werfen wir einen Blick darauf, wie sich das beim d’Hondt-Verfahren verhält. Das d’Hondt-Verfahren wurde vor 2013 zur Sitzzuteilung verwendet und erfreut sich bei Fachschaftswahlen noch großer Beliebtheit. Die beiden Verfahren funktionieren sehr, sehr ähnlich.

Wahrscheinlichkeit, dass d’Hondt fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)

Wir sehen ein etwas anderes Muster mit etwas extremeren Werten.

Die Grundtendenz ist aber offensichtlich: Je mehr Listen es gibt, desto wahrscheinlicher ist es, dass zwei oder mehrere Listen die gleiche Sitzzahl haben, und damit zusammenhängend ist es auch wahrscheinlicher, dass die Verfahren fehlschlagen. Mit Fehlschlagswahrscheinlichkeiten zwischen 20 und 30 Prozent, wie wir sie aktuell haben, will man aber eigentlich nicht arbeiten.

Wie wäre es denn, wenn wir das d’Hondt-Verfahren anwenden, sofern STLGS fehlschlägt?

Wahrscheinlichkeit, dass sowohl STLGS als auch d’Hondt fehlschlagen, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)

Besser, besser. Aber: Immer noch über zehn Prozent im für uns relevanten Bereich. Wenn das schon die Notlösung sein soll, dann sollte sie doch bitte verlässlich funktionieren. Eine neue Idee muss also her.

Beliebt ist auch die Idee, die Ausschussgröße einfach so lange um zwei zu erhöhen, bis kein Problem mehr auftritt. Wie gut das klappt, zeigt die folgende Animation.

Wahrscheinlichkeit, dass STLGS für alle versuchten Ausschussgrößen fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben). Markiert sind nach Satzung zulässige Ausschussgrößen und die aktuelle Listenzahl im SP.

Erst bei bis zu dreifacher Erhöhung der Ausschussgröße landen die Wahrscheinlichkeiten für relevante Größen im Ein-Prozent-Bereich. Damit würde ein Fünferausschuss zum Elferrat, ein Neunerausschuss hätte fünfzehn Mitglieder. So viele Personen kriegen die sowieso nicht zusammengewählt.

Aber weshalb dieser Fetisch für ungerade Ausschusssitzzahlen? Erstens kommt es bei Mehrheiten sowieso meistens darauf an, wer gerade nicht die Sitzung vergessen hat. Zweitens treffen Ausschüsse mit Entscheidungskompetenz in der Regel keine politischen Entscheidungen. Und drittens haben wir mit dem von der FK zu benennenden Mitglied ein Aliud, das die Gesamtausschussgrößen aktuell sowieso auf eine gerade Zahl bringt.

Statt Erhöhung um zwei wollen wir uns nun also eine Erhöhung um eins ansehen:

Wenn wir diese Zwischenschritte zulassen, sind wir bereits nach vier Schritten bei Werten unter einem Prozent im relevanten Bereich. Besser jedenfalls als die Erhöhung um zwei.

Eins jedoch muss hier angemerkt werden: Es müssen nur ein paar mehr Listen antreten und die dann ein sehr ungünstiges Ergebnis erreichen, und schon steigt die Ausschussgröße wieder auf 43. Eine alleinige Lösung kann die Anhebung der Ausschussgröße also nicht sein.

Rohdaten als ods-Datei herunterladen

Ein anderes Problem ist, dass Personen die Augen verschließen vor dem, was in Satzung und Geschäftsordnung steht. ↩
Aktuell nach Satzung erlaubte Ausschussgrößen sind 3,5,7 und 9. ↩

25. Februar 2014

Analyse: Wann werden wir vom Rüngler-Problem kalt erwischt?

Für kommenden Mittwoch ist zu einer SP-Sitzung geladen, auf der die Ausschüsse des Studierendenparlaments der Uni Bonn nach einem entsprechenden Ältestenratsbeschluss neu besetzt werden sollen; derweil streiten sich die Größen der Bonner Hochschulpolitik munter weiter bis in die nächste Instanz.

Doch ignorieren wir das alles mal und wenden uns der eigentlichen Frage zu: Wie problematisch ist das Rüngler-Problem?

Die Fakten

Das Studierendenparlament hat 43 Sitze. Die Ausschüsse des Studierendenparlaments werden auf Basis dieser Sitzverteilung besetzt, nach dem Sainte-Laguë/Schepers-Verfahren. Die Anzahl der Ausschussmitglieder ist zunächst einmal sinnigerweise ungerade. Die Satzung der Studierendenschaft sieht Ausschussgrößen von 3, 5, 7 und 9 vor. Eine SP-Mehrheit hat also mindestens 22 Sitze, eine Ausschussmehrheit entsprechend 2, 3, 4 oder 5.

Das Problem (Wiederholung)

In der aktuellen Besetzung hat das Studierendenparlament das Problem, dass die SP-Mehrheit von RCDS und Jusos mit 22 Sitzen in einem Fünferausschuss nur 2 Sitze besetzen kann, also keine Mehrheit in diesem Ausschuss hätte. Entsprechendes gilt für einen Neunerausschuss. Erklärbärartikel zum sog. “Rüngler-Problem”

Was tun?

Zunächst einmal wollen wir die Frage beantworten, mit welchen Wahlergebnissen wir eigentlich rechnen müssen. Da für unser Problem nicht die Identität der Listen, sondern nur das Verhältnis ihrer Sitzzahlen interessant ist, genügt es, die Sitzverteilungen absteigend sortiert zu berechnen. Ein kleines Python-Skript mit einer zehnfach verschachtelten For-Schleife erledigt dies für 2 bis 10 antretende Listen in erstaunlicherweise weniger als einer Sekunde¹. Wen diese Ergebnisse interessieren: klick.

Doch damit beginnt der große Spaß ja erst. Nun wird jede dieser Sitzverteilungen darauf geprüft, für welche Ausschussgrößen das Rüngler-Problem auftritt. Alternativ kann natürlich auch das Sainte-Laguë/Schepers-Verfahren zu viele Sitze zuteilen, was ebenfalls nicht wünschenswert, aber hier nicht primärer Gegenstand unserer Betrachtung ist.

Resultate

Ei, ei, ei.

Nehmen wir mal an, der RCDS hätte einen Sitz weniger und die Piraten-Hochschulgruppe einen Sitz mehr im Studierendenparlament. Abstrakt sieht das ganze also so aus:

Unsere Beispielverteilung.

Nun bilden wir unsere Ausschüsse mit dem bewährten Sainte-Laguë/Schepers-Verfahren. In den folgenden Grafiken markiert die gestrichelte Linie die Mitte. Alle Listen links und auf dieser Linie besitzen zusammen eine Mehrheit im Ausschuss.

Dreierausschuss

B+C: 21 SP-Sitze, haben jedoch Ausschussmehrheit

B+C: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem

Fünferausschuss

majority-05

A+D: Nur 16 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem

Siebenerausschuss

majority-07

B+C: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem

Neunerausschuss

majority-09

C+D+E+F: Nur 20 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem

Aber hey, es ist Karneval! Versuchen wir es doch mal mit einem Elferrat, dat hätt noch emmer joot jejange!

Elferausschuss (nicht satzungskonform)

majority-11

B+D+E+F: Nur 21 SP-Sitze, haben jedoch Ausschussmehrheit → Rüngler-Problem

Wat fott es, es fott. *hust*

Herr Doktor, wie schlimm isset?

Schlimmstenfalls treten bei der nächsten Wahl 8 Listen an und es ergibt sich folgendes Ergebnis:

Können wir das machen? Bitte?

Dann haben wir das Rüngler-Problem bei einer Ausschussgröße von 3. Und bei 5. Und bei 7. Und 9. Und 11. Und 13. Überhaupt bei jeder ungeraden Zahl zwischen 2 und 42 – außer bei 23: Da schlägt dann das Sainte-Laguë/Schepers-Verfahren fehl, weil fünf Listen gleichzeitig die letzten vier Sitze zugeteilt bekämen. Die Rüngler-Lösung, bei der einfach die Ausschussgröße so weit nach oben korrigiert wird, bis das Problem nicht mehr auftritt, würde also zu 43er-Ausschüssen führen – da kann man dann eigentlich gleich eine SP-Sitzung einberufen.

Nun haben wir Extrembeispiele gesehen. Blicken wir nun auf einen Graphen, der die Wahrscheinlichkeit abbildet, dass bei einer der vier von der Satzung vorgesehenen Ausschussgrößen das Rüngler-Problem auftritt, oder das Sainte-Laguë/Schepers-Verfahren (STLGS) nicht die gewünschte Zahl an Sitzen zuteilen kann.

Aufgeteilt wird das ganze nach der Anzahl der im SP vertretenen Listen.

Wir sehen: Je mehr Listen im SP sitzen, desto wahrscheinlicher wird es, dass das Sainte-Laguë/Schepers-Verfahren für eine der Ausschussgrößen fehlschlägt, und noch stärker steigt die Wahrscheinlichkeit, dass das Rüngler-Problem auftritt.

Eine Grafik hab ich noch: Wie wahrscheinlich ist es, dass für alle vier vorgesehenen Ausschussgrößen entweder das Rüngler-Problem auftritt oder das Sainte-Laguë/Schepers-Verfahren nicht die gewünschte Zahl an Sitzen zuteilen kann?

Sieht verschmerzbar aus. Wobei: 10 % sind eigentlich doch ganz schön viel. Anscheinend konvergiert das gegen 25 %, also jedes vierte Wahlergebnis wäre höchstproblematisch. Gegen zu viele Listen im SP könnte ja eine Sperrklausel bei der Wahl helfen *diabolisches Grinsen*

Fazit

Wenn das Rüngler-Problem ein Problem ist, ist es tatsächlich ein Problem.

So, für heute habe ich nun mit genug Zahlen und Bildern um mich geworfen. Das gesamte Team von hszemi.de wünscht allen Beteiligten viel Vergnügen bei der Lösung dieses Problems!

Disclaimer: Menschen machen Fehler. Falls ihr in den obigen Zahlen und Grafiken einen Fehler bemerkt, freue ich mich über einen Hinweis, zum Beispiel in den Kommentaren.

Für eine einzige Liste ist dies trivial. Beweis durch scharfes Hinschauen. (Für 2 Listen eigentlich ja auch.) ↩