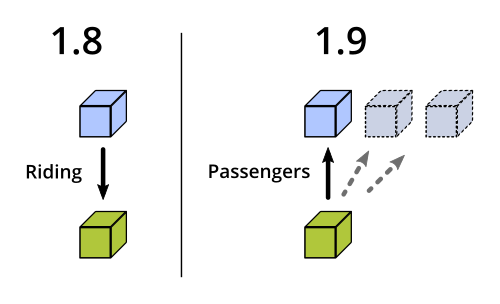
Wenn man – also nur hochtheoretisch – in Minecraft einen Wither im End spawnt1, und der dann durch das Portal entfleucht – ja dann ist das erstmal blöd. Weil er dann in der normalen Welt wieder auftaucht und dort wild um sich schießt. Macht Löcher in die Landschaft. Nicht hübsch.
Wenn man den dann wieder eingefangen und die gröbsten Schäden beseitigt hat, ergibt sich ein neues Problem: Kommt so ein Wither-Projektil an die Grenze eines Chunks, der nicht geladen ist, verschwindet es nicht einfach, sondern bleibt dort stehen. Theoretisch werden Projektile mit Geschwindigkeit 0 nicht angezeigt, aber nun ja, Theorie und Praxis haben an dieser Stelle nicht viel miteinander zu tun. Das heißt, man hat dann in etwa so einen Ausblick:
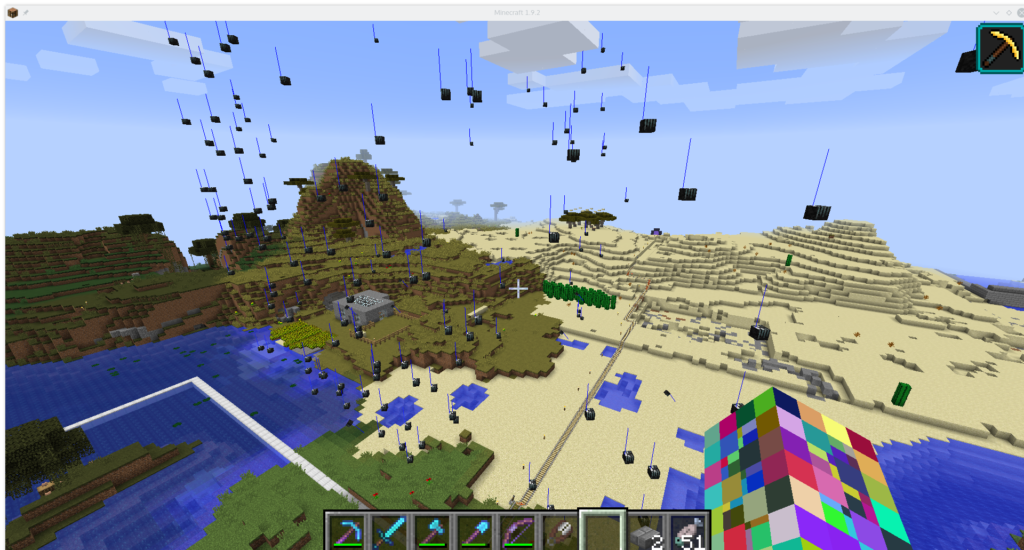
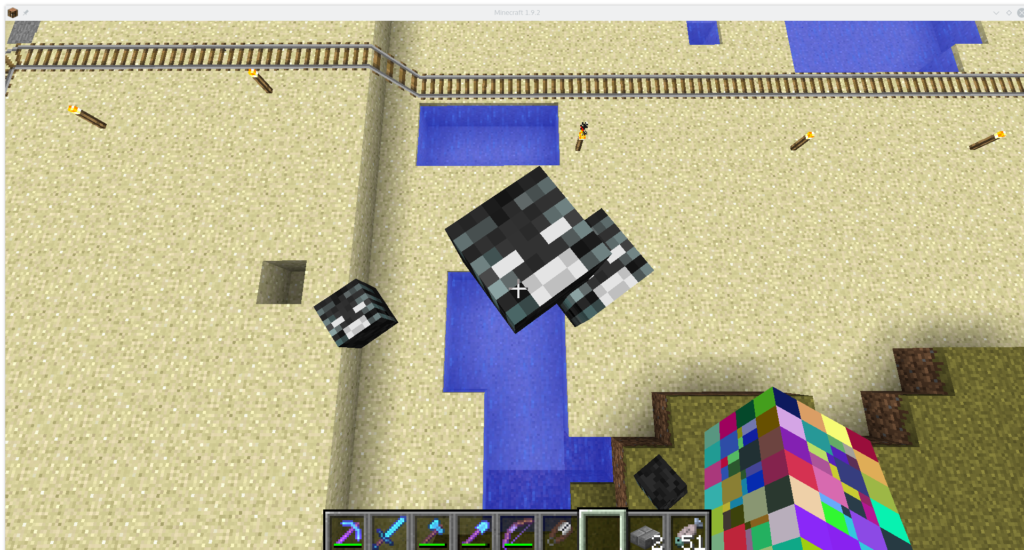
Hübsche Totenköpfe schweben in der Luft. Die blauen Linien sind die Blickrichtungen, angezeigt durch F3+B.
Die Krater in der Wüste im Hintergrund stammen übrigens vom entfleuchten Wither.
Die Totenköpfe haben keine Hitbox, das heißt man kann durch sie hindurchlaufen/fliegen, sie aber nicht schlagen. Mit einem Piston und einem Schleimblock können sie interessanterweise wieder beschleunigt werden. Bei so vielen Köpfen macht das aber keinen Spaß.
Kuckuck!
Los wird man die Totenköpfe, indem man (entsprechende Rechte vorausgesetzt) in der Eingabezeile folgendes eingibt:
/kill @e[type=WitherSkull]
Das “tötet” alle Entities vom Type WitherSkull. Und der Blick gen Himmel ist wieder unverstellt.
- Denglisch to the max! ↩