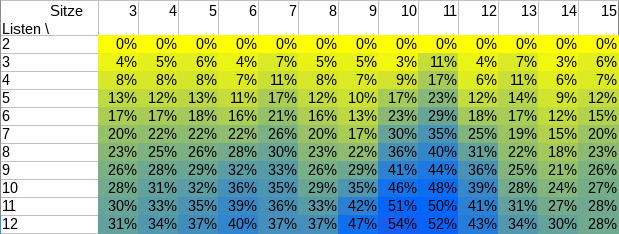
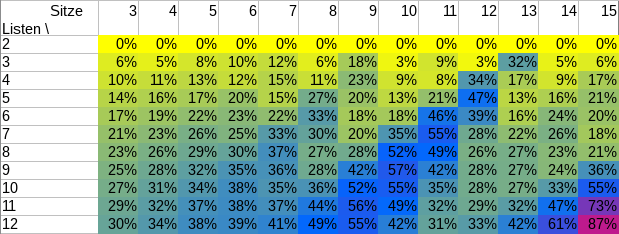
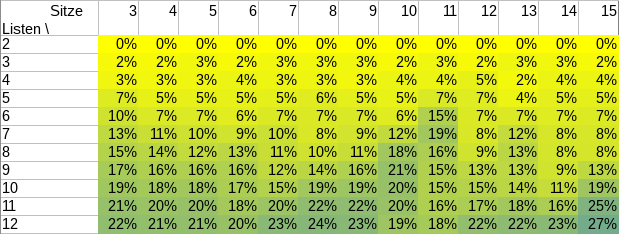
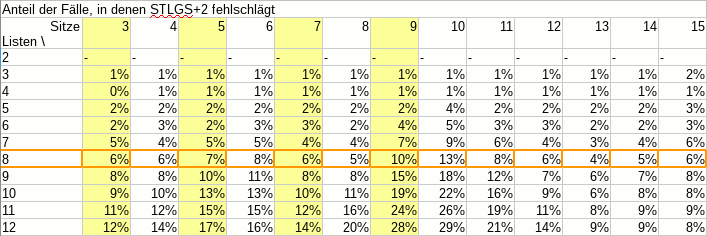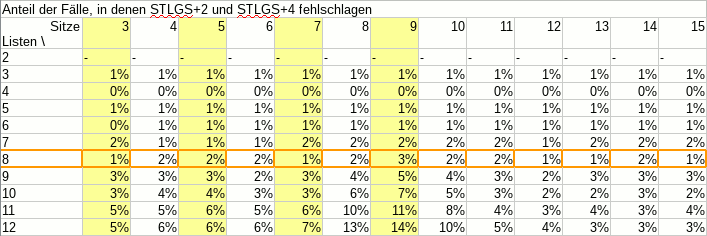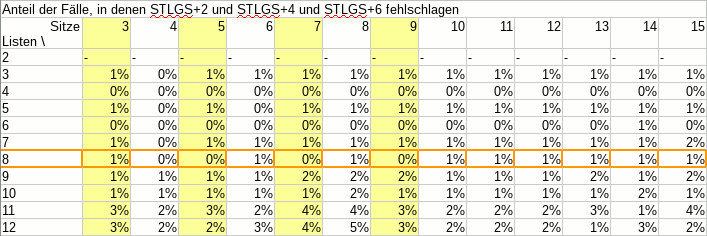
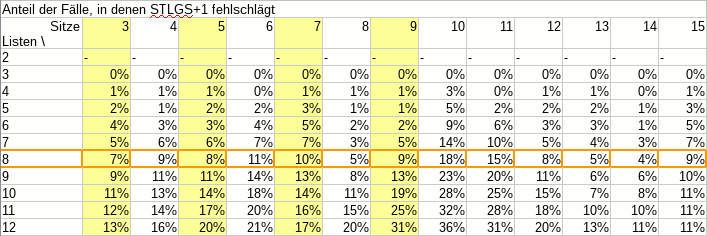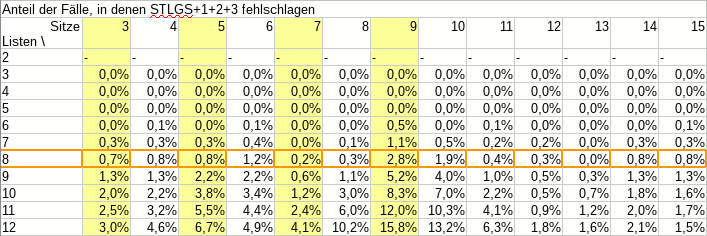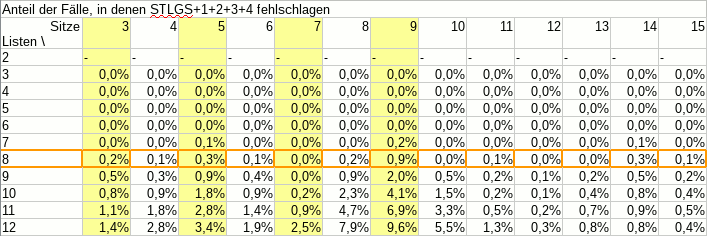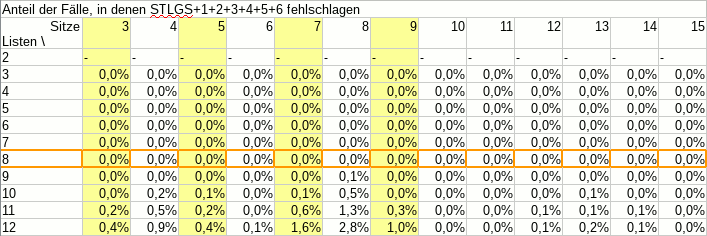
Als ich vor einem Dreivierteljahr eine Rolle Smarties® zählte, war das ganze recht unprofessionell, denn: Es fehlte eine Tabelle mit Zahlen. Und ohne Tabelle mit Zahlen, das ist klar, ist das ganze nicht wissenschaftlich.
Da auch die Reproduzierbarkeit bei wissenschaftlichen Untersuchungen sehr wichtig ist, erwarb ich im lokalen Einzelhandel eine weitere Rolle Smarties® und zählte wieder nach.
Das Studierendenparlament hat seine Ausschüsse nach mittlerweile zwei Monaten immer noch nicht voll besetzt. Eins der Probleme1 ist, dass das zur Sitzzuteilung verwendete Sainte-Laguë/Schepers-Verfahren nicht für jede SP-Besetzung eindeutige Ausschussbesetzungen erzeugen kann. Besonders häufig tritt das Problem auf, wenn Fraktionen im Parlament die selbe Sitzzahl haben und dann bei Zuteilung des letzten Sitzes gleichzeitig “an der Reihe” wären.
Oft wird und wurde vorgeschlagen, dann die Sitzzahl im Ausschuss einfach zu erhöhen. Wie erfolgsversprechend das ist, wollen wir heute betrachten.
Zunächst stellt sich die Frage, wie häufig das Problem überhaupt auftritt. Ich habe also die Wahrscheinlichkeit berechnet, dass das Sainte-Laguë/Schepers-Verfahren (im folgenden STLGS) fehlschlägt, und zwar für 2-12 vertretene Listen und Ausschussgrößen von 3 bis 152.
Wahrscheinlichkeit, dass STLGS fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)
Zum Vergleich werfen wir einen Blick darauf, wie sich das beim d’Hondt-Verfahren verhält. Das d’Hondt-Verfahren wurde vor 2013 zur Sitzzuteilung verwendet und erfreut sich bei Fachschaftswahlen noch großer Beliebtheit. Die beiden Verfahren funktionieren sehr, sehr ähnlich.
Wahrscheinlichkeit, dass d’Hondt fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)
Wir sehen ein etwas anderes Muster mit etwas extremeren Werten.
Die Grundtendenz ist aber offensichtlich: Je mehr Listen es gibt, desto wahrscheinlicher ist es, dass zwei oder mehrere Listen die gleiche Sitzzahl haben, und damit zusammenhängend ist es auch wahrscheinlicher, dass die Verfahren fehlschlagen. Mit Fehlschlagswahrscheinlichkeiten zwischen 20 und 30 Prozent, wie wir sie aktuell haben, will man aber eigentlich nicht arbeiten.
Wie wäre es denn, wenn wir das d’Hondt-Verfahren anwenden, sofern STLGS fehlschlägt?
Wahrscheinlichkeit, dass sowohl STLGS als auch d’Hondt fehlschlagen, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben).
Farbkodierung Gelb (0%) – Blau (50%) – Rot (100%)
Besser, besser. Aber: Immer noch über zehn Prozent im für uns relevanten Bereich. Wenn das schon die Notlösung sein soll, dann sollte sie doch bitte verlässlich funktionieren. Eine neue Idee muss also her.
Beliebt ist auch die Idee, die Ausschussgröße einfach so lange um zwei zu erhöhen, bis kein Problem mehr auftritt. Wie gut das klappt, zeigt die folgende Animation.
Wahrscheinlichkeit, dass STLGS für alle versuchten Ausschussgrößen fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben). Markiert sind nach Satzung zulässige Ausschussgrößen und die aktuelle Listenzahl im SP.
Erst bei bis zu dreifacher Erhöhung der Ausschussgröße landen die Wahrscheinlichkeiten für relevante Größen im Ein-Prozent-Bereich. Damit würde ein Fünferausschuss zum Elferrat, ein Neunerausschuss hätte fünfzehn Mitglieder. So viele Personen kriegen die sowieso nicht zusammengewählt.
Aber weshalb dieser Fetisch für ungerade Ausschusssitzzahlen? Erstens kommt es bei Mehrheiten sowieso meistens darauf an, wer gerade nicht die Sitzung vergessen hat. Zweitens treffen Ausschüsse mit Entscheidungskompetenz in der Regel keine politischen Entscheidungen. Und drittens haben wir mit dem von der FK zu benennenden Mitglied ein Aliud, das die Gesamtausschussgrößen aktuell sowieso auf eine gerade Zahl bringt.
Statt Erhöhung um zwei wollen wir uns nun also eine Erhöhung um eins ansehen:
Wahrscheinlichkeit, dass STLGS für alle versuchten Ausschussgrößen fehlschlägt, in Prozent, für Anzahl der im SP vertretenen Listen (links) und Ausschussgröße (oben). Markiert sind nach Satzung zulässige Ausschussgrößen und die aktuelle Listenzahl im SP.
Wenn wir diese Zwischenschritte zulassen, sind wir bereits nach vier Schritten bei Werten unter einem Prozent im relevanten Bereich. Besser jedenfalls als die Erhöhung um zwei.
Eins jedoch muss hier angemerkt werden: Es müssen nur ein paar mehr Listen antreten und die dann ein sehr ungünstiges Ergebnis erreichen, und schon steigt die Ausschussgröße wieder auf 43. Eine alleinige Lösung kann die Anhebung der Ausschussgröße also nicht sein.
Wir können uns die kommenden Wahlen zum XXXVIII. Studierendenparlament sparen und einfach das Ergebnis von 2011 recyceln.
Wieso? Daso:
Die Zahl der zur Wahl antretenden Listen nahm in den vergangenen Jahren fortwährend ab, zur Wahl 2016 haben wir einen sprunghaften Anstieg. Auf den Stand von 2011.
Auch bei der Gesamtzahl der Kandidierenden war die Tendenz in den letzten Jahren klar fallend – zur Wahl 2016 haben wir einen sprunghaften Anstieg. In etwa auf den Stand von 2011.
Bei den Listen, die zur Wahl des 33. Studierendenparlaments antraten, sind unterschiedliche Trends zu erkennen: Die Kandidierendenzahl von RCDS und LUST geht zurück und erholt sich dann wieder, bei GHG und PHG beobachten wir einen entgegengesetzten Effekt, und einzig die JUSOS hopsen wild auf und ab – alle, um zur Wahl 2016 wieder auf dem Ausgangswert von 2011 zu landen.
Ist der Bologna-Knick überwunden? Haben plötzlich wieder mehr Studierende Lust auf Hochschulpolitik? Man weiß es nicht. Was man aber weiß: Wenn auch noch die Wahlbeteiligung von 2011 kopiert wird (17,0 %), reicht das für die beiden Urabstimmungen nicht aus.
