Jedes Jahr nach der Studierendenparlamentswahl haben wir Spaß mit der Besetzung der Ausschüsse1,2. Mittlerweile kann man fast die Uhr, pardon, den Kalender danach stellen.
Was sind SP-Ausschüsse?
Das SP kann zur Vorbereitung und Unterstützung seiner Arbeit und für Untersuchungen ständige oder nichtständige Ausschüsse einsetzen. Die Zahl der Mitglieder eines Ausschusses beträgt drei, fünf, sieben oder neun.3
Diese “ständigen” Ausschüsse, die jedes Jahr gewählt werden, sind der Wahlausschuss und der Wahlprüfungsausschuss, der Haushaltsausschuss, der eine Stellungnahme zum Haushaltsplan abgibt, der Kassenprüfungsausschuss, der genau das tut, was sein Name verspricht; Ausschüsse für Hilfsfonds, Rechtshilfefonds und Semesterticketrückerstattung, sowie der Satzungs- und Geschäftsordnungsausschuss. Als “nichtständige” Ausschüsse hingegen gab es in den vergangenen Jahren beispielsweise den Unicardausschuss oder einen Untersuchungsausschuss, die die Arbeit des Parlaments ihrerseits in ihrem speziellen Aufgabenbereich vorbereitet und unterstützt haben.
Wo liegt diesmal das Problem?
Die Ausschussmitglieder werden gemäß Satzung der Studierendenschaft und Geschäftsordnung des SP von den Fraktionen vorgeschlagen. Dabei ist, wie die Satzung vorschreibt, “nach dem Sainte-Laguë/Schepers-Verfahren das Stärkeverhältnis aufgrund der Sitze im SP zugrunde zu legen”. Das Sainte-Laguë/Schepers-Verfahren ist ein lustiges Verfahren zur Sitzzuteilung bei Verhältniswahlen, das jedes Jahr aufs neue in der Wahlzeitung anhand eines kleinen Beispiels erklärt wird. Alternativ hilft Wikipedia.
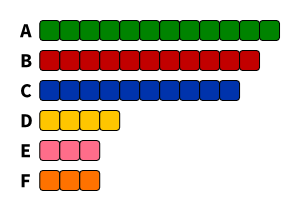
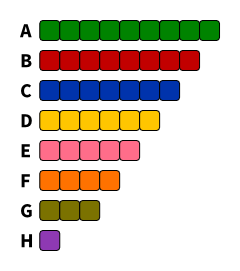
Zur Berechnung, welche Fraktion wie viele Ausschusssitze besetzen darf, benötigen wir zunächst das Wahlergebnis4:
| Liste | Sitze |
|---|---|
| JUSOS | 10 |
| RCDS | 10 |
| LUST | 3 |
| LHG | 5 |
| PHG | 1 |
| LISTE | 3 |
| GHG | 8 |
| KULT | 3 |
Dann wollen wir mal Sitze zuteilen!
| Divisor | JUSOS | RCDS | LUST | LHG | PHG | LISTE | GHG | KULT |
| 10 | 10 | 3 | 5 | 1 | 3 | 8 | 3 | |
| 0,5 | 20,0 | 20,0 | 6,0 | 10,0 | 2,0 | 6,0 | 16,0 | 6,0 |
| 1,5 | 6,7 | 6,7 | 2,0 | 3,3 | 0,7 | 2,0 | 5,3 | 2,0 |
| 2,5 | 4,0 | 4,0 | 1,2 | 2,0 | 0,4 | 1,2 | 3,2 | 1,2 |
Was benötigen wir? Zunächst nur einen Siebener-Ausschuss und ein paar Fünfer-Ausschüsse. Und irgendwann noch einen Neuner-Ausschuss.
Die ersten vier Sitze (gelb hinterlegt) gehen ganz klar an JUSOS, RCDS, LHG und GHG. Doch der fünfte Sitz (lila) ginge gleichzeitg an JUSOS oder RCDS. Was in diesem Fall zu tun ist, regeln aktuell weder Satzung noch Geschäftsordnung. Wir ignorieren das Problem an dieser Stelle also auch fürs Erste und hoffen, dass wir beim Siebener-Ausschuss mehr Glück haben.
Vier gelbe Sitze, zwei lila Sitze, macht insgesamt sechs, und dann nur noch einen… Na bravo. Der letzte Sitz im Siebener-Ausschuss geht gleichzeitig an LUST, LISTE und KULT. Wer ihn bekommt? Nicht geregelt.
Wenigstens im Neunerausschuss gibt es kein Problem. Da bekommen bis auf die Piraten-Hochschulgruppe5 alle Fraktionen einen Sitz, JUSOS und RCDS zwei.
Hatte ich bereits erwähnt, dass hier eine SP-Mehrheit aus RCDS, GHG und LHG (23/43 Sitze) keine Ausschussmehrheit mehr stellt (4/9 Sitze)? Und jährlich grüßt das Rünglertier.
Eine Lücke! Eine Lücke!
Doch zurück zum eigentlichen Thema dieses Beitrags. Aktuell ist nicht geregelt, wie mit der Höchstzahlgleichheit6 im Fünfer- und Siebenerausschuss umzugehen ist. Mehrere Alternativen sind spontan denkbar:
- Losen. In der Wahlordnung ist bereits geregelt, dass bei der Verteilung der SP-Sitze auf die Listen gelost wird, falls bei den letzten Sitzen Höchstzahlgleichheit auftritt. Der Nachteil, falls das auf die Ausschüsse übertragen wird: Eine Fraktion könnte mehrfach durch Los den letzten Sitz erhalten, was unfair gegenüber den übrigen Fraktionen wäre, die ja grundsätzlich den gleichen Anspruch auf den letzten Sitz hätten.
- Zuteilung anhand der Stimmzahlen. Statt quasi ein zweistufiges Sainte-Laguë/Schepers-Verfahren durchzuführen (Stimmen -> SP-Sitze -> Ausschusssitze), werden die Sitze direkt aus den Stimmverhältnissen errechnet. Das Problem hierbei: Fraktionen müssen nicht zwingend den zur Wahl angetretenen Listen entsprechen. Außerdem stünde die Regelung im Widerspruch zur Satzung, die ja explizit vom “Stärkeverhältnis aufgrund der Sitze im SP” spricht.
- Die Sitze unbesetzt lassen. Die aktuelle Übergangslösung: Die strittigen Sitze werden erst einmal nicht besetzt. Sicher nicht im Sinne des Erfinders, und insbesondere benachteiligt es die kleinen Listen, die so gar keinen Sitz in den Ausschüssen haben.
- Die Ausschüsse vergrößern, bis es passt. Was vor zwei Jahren schon nicht erlaubt war, kann man doch einfach noch einmal vorschlagen, oder? Leider ist nicht einmal garantiert, dass das mit dem Vergrößern unterhalb einer Ausschussgröße von 43 irgendwann aufhört.
Exkurs: Told you so
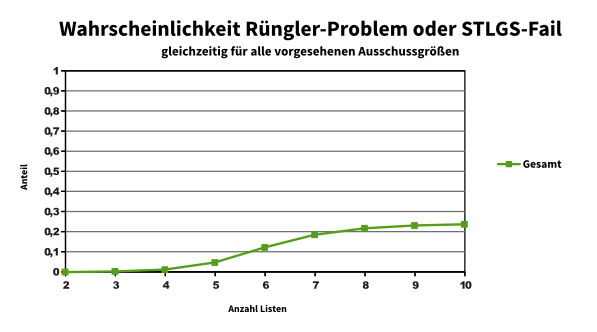
Blicken wir auf eine Infografik aus dem Jahr 2014:
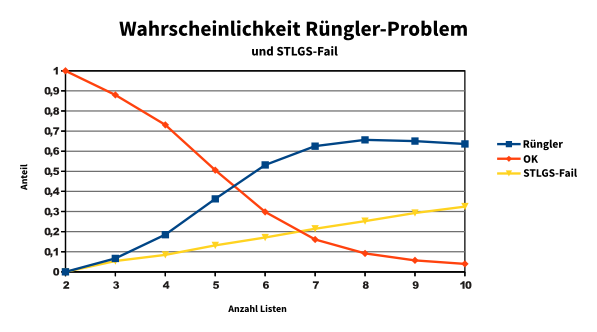
Aufgeteilt wird das ganze nach der Anzahl der im SP vertretenen Fraktionen.
Wir sehen: Je mehr Fraktionen im SP vertreten sind, desto wahrscheinlicher wird es, dass das Sainte-Laguë/Schepers-Verfahren für mindestens eine Ausschussgröße nicht mehr eindeutig bestimmt, welche Fraktionen wie viele Sitze besetzen dürfen (hier knackig als “STLGS-Fail” bezeichnet). Und diese Wahrscheinlichkeit ist auch nicht vernachlässigbar. Eine Regelung für diesen Fall muss her.
Eine faire Regel…
Attraktiv am Losentscheid ist, dass er eine enorme Objektivität ausstrahlt, keine externen Abhängigkeiten hat und am Ende niemand schuld ist. Unfair erscheint die ganze Sache erst, wenn Plätze in mehreren Ausschüssen ausgelost werden und immer die gleiche Fraktion zufällig den Zuschlag erhält. Dem könnte man dadurch begegnen, dass am Losentscheid nur die Listen teilnehmen, die bislang am wenigsten Ausschusssitze durch Los zugeteilt bekommen haben.
Das hieße allerdings wieder, dass plötzlich relevant würde, in welcher Reihenfolge die Ausschüsse besetzt werden. Beispielsweise könnten RCDS und JUSOS dann nur entweder für den Kassenprüfungsausschuss (KPA, 5 Mitglieder) oder den Wahlprüfungsausschuss (WPA, 5 Mitglieder) zwei Mitglieder benennen: Bekommen sie den zweiten Sitz im KPA zugelost, erhält automatisch die andere Fraktion den Sitz im WPA.
Auch dieses Problem lässt sich lösen, und zwar indem die Reihenfolge, in der die Ausschusssitze verlost werden, ebenfalls randomisiert wird. Gewählt werden kann dann ja immer noch in der in der Tagesordnung vorgegebenen Reihenfolge.
Was kann nun noch passieren? Eine Fraktion könnte zwar einen Sitz zugelost bekommen, aber gar niemanden dafür vorschlagen wollen. In dem Fall bliebe der Sitz erst einmal unbesetzt, obwohl möglicherweise die anderen Fraktionen Vorschläge für die Besetzung gehabt haben könnten. Getreu dem Motto “Lieber ein Ausschussmitglied als kein Ausschussmitglied” sollte der freibleibende Sitz dann neu verlost werden.
Ideal wäre es ja, wenn die Fraktionen sich von sich aus auf eine Besetzung einigen könnten. Versuchen kann man es ja einmal.
…und ihre Formulierung
Das mag jetzt alles recht sinnvoll geklungen haben, aber für eine Geschäftsordnungsregelung ist es viel zu lang. Kurz und leicht umsetzbar sollte es sein.
Hier ein Vorschlag zur Ergänzung von § 41 der SP-Geschäftsordnung:
(2) Würde das Sainte-Laguë/Schepers-Verfahren mehr Sitze zuteilen als ein Ausschuss Sitze hat, so sollen die Fraktionen, die rechnerisch Anspruch auf die Besetzung der strittigen Sitze hätten, sich auf einen gemeinsamen Vorschlag einigen. Kann keine Einigung erzielt werden, so werden die strittigen Sitze unter den anspruchsberechtigten Fraktionen verlost. Dabei sind zunächst die Fraktionen zu berücksichtigen, die bislang die wenigsten Ausschusssitze auf diese Weise zugelost bekommen haben. Werden auf einer Sitzung mehrere Ausschüsse besetzt, erfolgt die Verlosung in zufälliger Reihenfolge. Kann eine Fraktion einen ihr auf diese Weise zugelosten Sitz nicht besetzen, wird er erneut unter den übrigen anspruchsberechtigten Fraktionen in der ursprünglichen Reihenfolge verlost.
Mal sehen, was das SP daraus macht.
- Analyse: Wann werden wir vom Rüngler-Problem kalt erwischt? (2014) ↩
- Rüngler ist zurück (2015) ↩
- Das ist jetzt § 12 Abs. 1 der Satzung der Studierendenschaft, wörtlich übernommen. ↩
- Wir gehen davon aus, dass jede Liste im SP ihre eigene Fraktion bildet. Letztlich ist es aber für unser Problem egal, wie die Fraktionen entstehen. Die PHG kann übrigens keine eigene Fraktion bilden, dafür bräuchte es nämlich zwei Personen. ↩
- die allein sowieso keine Fraktion bilden können. Details, Details! ↩
- Die größte noch nicht berücksichtigte Zahl in der Tabelle ist die “Höchstzahl”. ↩