Die Bachelorprüfungsordnung für den Studiengang B.Sc. Informatik an der Uni Bonn sagt in § 11:

(6) In Lehrveranstaltungen (mit Ausnahme von Vorlesungen), in denen das Qualifikationsziel nicht anders erreicht werden kann, kann der Prüfungsausschuss auf Antrag eines Lehrenden die regelmäßige/erfolgreiche/aktive Teilnahme als Voraussetzung für die Zulassung zur Modulprüfung festlegen. Dabei ist zu definieren, wann eine regelmäßige/erfolgreiche/aktive Teilnahme vorliegt. Die Entscheidung ist gemäß § 6 Abs. 6 bekanntzugeben.

Das funktioniert also folgendermaßen: Die Lehrperson stellt einen Antrag an den Prüfungsausschuss. In diesem Antrag steht, was die Studierenden tun müssen, um zur Klausur zugelassen zu werden. Etwa einen bestimmten Anteil an Übungsaufgaben lösen und vorstellen. Und dann wird das begründet, in der Regel mit “Sonst lernen die Kleinen keine Softskills und würden sich wissenschaftlich fehlverhalten”¹.

Manche Informatikmodule werden jedoch von Professoren der diskreten Mathematik² gehalten. Die Mathematik in Bonn, muss man wissen, ist gar überaus exzellent. Nur merkt man das nicht immer.

Blicken wir noch einmal auf obigen Absatz 6:

[…] Dabei ist zu definieren, wann eine regelmäßige/erfolgreiche/aktive Teilnahme vorliegt. […]

Und nun auf ein Paar Studienleistungen aus dem letzten Wintersemester.

Prof. Dr. Stefan Hougardy
Modul: BA-INF 107 Einführung in die Diskrete Mathematik

Erforderliche Studienleistungen gemäß § 11 (6) PO:
50 % der Übungspunkte, sowie regelmäßige, aktive Teilnahme an den Übungsgruppen. Die Bearbeitung der Übungsaufgaben kann in Gruppen bis zur Größe 2 erfolgen. Bei Abgaben in Gruppen muss jeder Teilnehmer in der Lage sein, alle abgegebenen Lösungen seiner Gruppe zu erklären.

Die regelmäßige/erfolgreiche/aktive Teilnahme liegt also vor, wenn man regelmäßig, aktiv teilnimmt. Und 50 % der Punkte erreicht. Genial! Und so exzellent definiert.

Was verlangte denn sein Kollege?

Dr. Nicolai Hähnle
Modul: BA-INF 106 Lineare und ganzzahlige Optimierung

Erforderliche Studienleistungen gemäß § 11 (6) PO:
50 % der Übungspunkte, sowie regelmäßige, aktive Teilnahme an den Übungsgruppen. Die Bearbeitung der Übungsaufgaben kann in Gruppen bis zur Größe 3 erfolgen. Bei Abgaben in Gruppen muss jeder Teilnehmer in der Lage sein, alle abgegebenen Lösungen seiner Gruppe zu erklären.

Huch! Sehen wir hier beim exzellenten Mathematiker etwa eine ungekennzeichnete Textübernahme³? Natürlich nicht. Die maximale Gruppengröße ist schließlich 3, nicht 2. Eine insgesamt ebenbürtige Studienleistung.

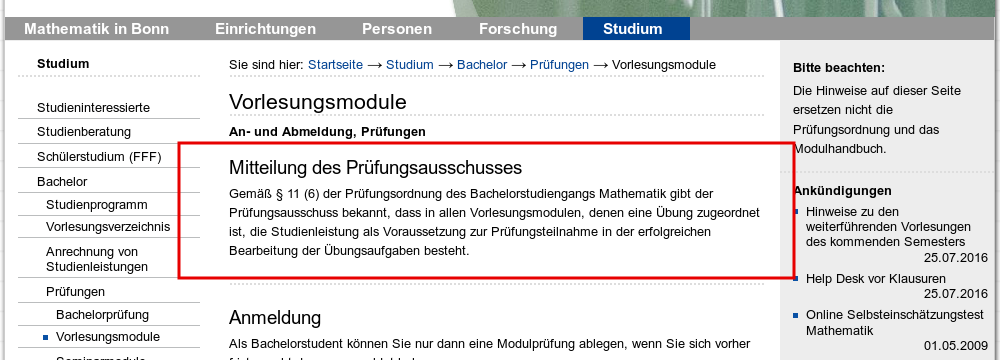
Generell hat die Mathematik in Bonn ein laxe Herangehensweise an Studienleistungen. Auf der Webseite der Mathematik steht aktuell zu lesen:

Was auch immer “erfolgreich” heißt. Immer noch besser jedenfalls als das, was dort noch im letzten Jahr⁴ zu lesen war:

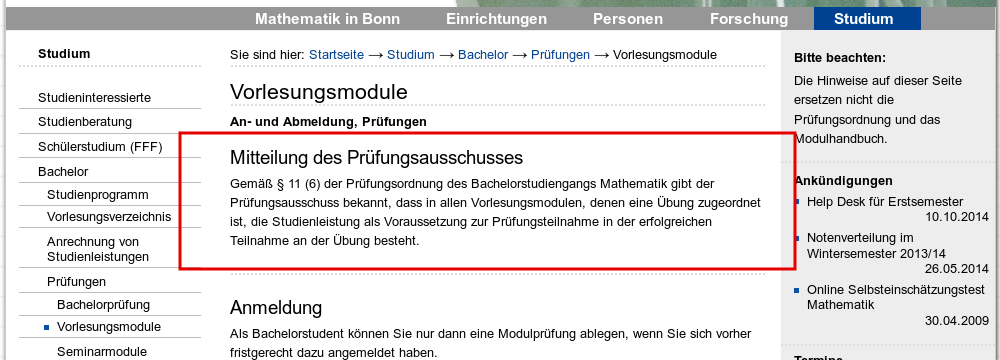
Jaja, die “erfolgreiche” Teilnahme, bei der man aber nicht sagen will, was “erfolgreich” heißt. Sehr lustig. Wenn wir uns im Kindergarten befinden. Bei einer Behörde im Sinne des Verwaltungsverfahrens- und Verwaltungsprozessrechtes wirkt diese Yolo-Attitüde was Studienleistungen angeht allerdings eher befremdlich.

Das mit der “erfolgreichen Teilnahme” fanden die Mathematikerinnen und Mathematiker so toll, dass sie es sogar in ihre Prüfungsordnung von 2012 geschrieben haben (§ 11):

(6) In Lehrveranstaltungen (mit Ausnahme von Vorlesungen), in denen das Qualifikationsziel nicht anders erreicht werden kann, kann der Prüfungsausschuss auf Antrag eines Lehrenden oder Modulbeauftragten die regelmäßige/ aktive/ erfolgreiche Teilnahme als Voraussetzung für die Teilnahme an der Modulprüfung festlegen. Dabei ist zu definieren, wann eine regelmäßige/ aktive/ erfolgreiche Teilnahme vorliegt. Die Entscheidung ist vom Prüfungsausschuss gemäß § 6 Abs. 9 bekanntzugeben.
Da das Verständnis für mathematische Sachverhalte nur durch gemeinsames Lernen und aktives Lösen von Aufgaben im Austausch mit anderen Studierenden und dem Dozenten optimal erreicht werden kann, wird bei allen Übungen, die zu Vorlesungen gehören, eine erfolgreiche Übungsteilnahme als Zulassungsvoraussetzung für die Klausur oder Mündliche Prüfung verlangt.

(Hervorhebung von mir)

Was unter der “erfolgreichen” Übungsteilnahme zu verstehen ist, steht da aber natürlich nicht.
Die persönliche Anwesenheit der Studierenden kann es schon einmal nicht sein, da das Hochschulgesetz seit 2014 explizit verbietet, so etwas in einer allgemeinen Regel festzulegen⁵. Ein Teil der Begründung hierfür ist bemerkenswert, wenn man ihn mit dem markierten Teil von § 11 Abs. 6 vergleicht:

Mit der Regelung⁶ soll zudem die Eigenverantwortlichkeit der Studierenden gestärkt und der Umstand unterstrichen werden, dass hochschulische Lehre in einer Gemeinschaft der Lehrenden und Lernenden stattfindet; Anwesenheitsobliegenheiten sind mit diesem Prinzip der Gemeinschaftlichkeit grundsätzlich nicht verträglich.

Aber was kümmert uns schon, was in irgend einer Gesetzesbegründung steht, gell.