In den Ausschüssen des Studierendenparlaments geht es um Macht, Einfluss, Geld – oder auch nur um die UniCard.
Die Satzung der Studierendenschaft sieht vor, dass auf der konstituierenden Sitzung eines neuen Studierendenparlaments mindestens 7 Ausschüsse gewählt werden1. Sechs dieser 7 Ausschüsse haben 5 Mitglieder, der Haushaltsausschuss hat 7 Mitglieder.
Und dann sagt Absatz 6 in § 12 der Satzung folgendes:
(6) Bei Besetzung der Ausschüsse ist nach dem Sainte-Laguë/Schepers-Verfahren das Stärkeverhältnis aufgrund der Sitze im SP zugrunde zu legen.
Zur Erinnerung: Ihr habt demletzt folgendes SP gewählt:
| Liste | Sitze |
|---|---|
| GHG | 12 |
| JUSOS | 11 |
| RCDS | 11 |
| LHG | 4 |
| LUST | 3 |
| PIRATEN | 2 |
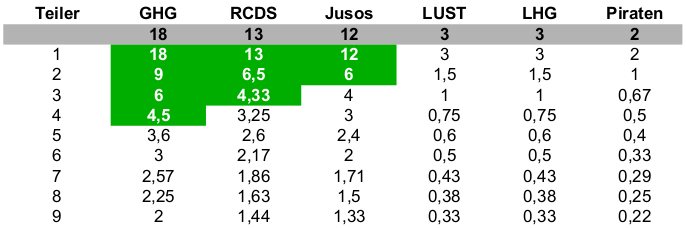
Nun haben Experten von RCDS und Juso-Hochschulgruppe folgendes festgestellt: Rechnerisch hätten diese beiden Gruppen zusammen eine hauchdünne Mehrheit von 22 Sitzen im SP. Bildet man jedoch nach Satzungsvorschrift einen Fünferausschuss, kommt dabei folgendes heraus:
| Liste | Sitze |
|---|---|
| GHG | 2 |
| JUSOS | 1 |
| RCDS | 1 |
| LHG | 1 |
Das bedeutet: Die SP-Mehrheit von Jusos und RCDS hätte in einem Fünferausschuss alleine keine Mehrheit! Dumm, dass fast alle Ausschüsse laut Satzung Fünferausschüsse sind.
Praktischerweise sieht die ganze Sache bei einem Ausschuss mit 7 Mitgliedern bereits anders aus – hier stellt die RCDS-Juso-SP-Mehrheit auch eine Ausschussmehrheit:
| Liste | Sitze |
|---|---|
| GHG | 2 |
| JUSOS | 2 |
| RCDS | 2 |
| LHG | 1 |
Zur konstituierenden Sitzung wurde also von Vertretern des RCDS und der Juso-Hochschulgruppe ein Antrag eingebracht, der die in Fünferausschüssen entstehende Situation als verfassungswidrig (!) einstufte und als Abhilfe eine Lösung vorschlug, die ich im Folgenden als Rüngler-Lösung bezeichnen werde, das zugehörige Problem als Rüngler-Problem: Abweichend von der Satzung sollten alle zu wählenden Ausschüsse mit 7 Personen besetzt werden.
Der Rest des Bönn’schen Parlamentarismus war erstaunt, mit welcher Leichtigkeit hier die Satzung ingoriert wurde (und ist es immer noch). Kurzversion: Der Antrag auf “Korrektur” der Ausschussgrößen wurde mit Mehrheit beschlossen, die Ausschüsse wurden mit je 7 Personen besetzt, es wurde protestiert. Die gemeinsame Stellungnahme von GHG, LHG und Piraten-HSG kann man sich wahlweise bei der GHG oder bei der LHG durchlesen. 2 Der Ältestenrat kann sich fürwahr nicht über Arbeitsmangel beklagen.
Kommen wir nur zur Gretchenfrage.
Hülft dat wat?
Ja. Im nach dem Sainte-Laguë/Schepers-Verfahren mit 7 Mitgliedern besetzten Ausschuss ist eine SP-Mehrheit auch eine Ausschussmehrheit – wenn alle da sind und niemand dazwischenfunkt – dazu später mehr.
Die 7 ist jedoch kein Allheilmittel. Genau genommen gibt es keine Zahl an Ausschussplätzen, für die die Wahlberechtigten sich nicht eine Wahlergebnis basteln können, das zum Rüngler-Problem führt.3 Ach doch: 1 und 43. (Es gibt sogar einen Ausschuss mit 43 Mitgliedern. Den Ferienausschuss. Das ist auch so ein lustiges Gremium.)
Schauen wir uns das mal an einem einfachen Beispiel an: Die Satzung sieht also Ausschüsse mit 5, 7 oder 9 Mitgliedern vor.
Gegeben sei folgendes Wahlergebnis:
| Liste | Sitze |
|---|---|
| A | 22 |
| B | 5 |
| C | 5 |
| D | 5 |
| E | 4 |
| F | 2 |
Im SP hat also Liste A (hier Grün dargestellt) die absolute Mehrheit:
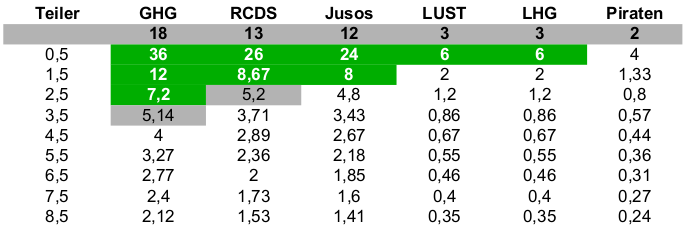
Wie sehen die nach Sainte-Laguë/Schepers verteilten Ausschüsse aus?
Neunerausschuss: (A-5,B-1,C-1,D-1,E-1) -> Okay!
Für diese Konstellation wäre also eine Aufstockung aller Ausschüsse auf 9 Mitglieder eine Lösung des Rüngler-Problems. Mit sieben Mitgliedern klappt es nicht.
-Einschub-
Es gibt bereits einen Ausschuss mit 9 Mitgliedern. Den Wahlausschuss. Raten Sie mal, für welchen Ausschuss sich in den letzten Jahren NIE genug Mitglieder gefunden haben, geschweige denn Stellvertreter?4
-Ende Einschub-
Doch auch die 9 ist kein Allheilmittel. Nimmt man Liste E einen Sitz weg und gibt ihn Liste F, so sieht der Neunerausschuss folgendermaßen aus:
Hurra.
Wir sehen also: Die Rüngler-Lösung löst das Rüngler-Problem nur im Einzelfall.
Man müsste also für jedes Wahlergebnis prüfen, in welchen Ausschussgrößen man Mehrheiten abseits der SP-Mehrheiten bilden kann, und diese dann auf die entsprechend höhere Zahl aufstocken, bei der das Problem nicht mehr auftritt. Und das ganze sollte dann noch in der Satzung verankert werden.
Der Witz an der ganzen Sache
Also nehmen wir mal an, eine SP-Mehrheit hätte ein gottgegebenes Recht5 auf eine Ausschussmehrheit. Und deshalb implementiert man eine funktionierende Lösung für das Rüngler-Problem.
Dann liest man Paragraph 12 Absatz 7 der Satzung der Studierendenschaft. Und fängt laut an zu lachen.
(7) Außer den nach Maßgabe der Abs. 1 bis 6 bestimmten Mitgliedern gehören jedem SP-Ausschuss zusätzlich ein ordentliches Mitglied und ein entsprechendes stellvertretendes Mitglied an, das nicht von den Fraktionen im SP, sondern von der FK zu benennen und durch das SP zu bestätigen ist. […]
Die Fachschaftenkonferenz kann also in jeden Ausschuss ein stimmberechtigtes Mitglied entsenden.
Aus dem Siebenerausschuss der Rüngler-Lösung wird somit ein Achterausschuss, in dem Abstimmungen theoretisch 4:4 ausgehen können. Und wieder hat eine SP-Mehrheit nicht mehr automatisch eine Ausschussmehrheit.
Ich bin mal gespannt, wie sie das Problem lösen wollen. Ich habe da schon so eine Ahnung. Sofern es denn überhaupt ein Problem ist.
Epilog
Das Sainte-Laguë/Schepers-Verfahren hat noch eine weitere nette Eigenschaft: Es kann leicht passieren, dass zwei oder mehr Listen zur selben Zeit den letzten Sitz zugeteilt bekämen. Man würde also entweder zu viele Sitze verteilen oder losen müssen. Ob das Rüngler-Problem in diesem Fall auch auftreten kann, fragen Sie?
Ich bitte Sie.
Sonst wär’s ja langweilig.
Weiterführende Links
Die Wikipedia-Seite zum Sainte-Laguë/Schepers-Verfahren: klick
Ein Rechner, der das Sainte-Laguë/Schepers-Verfahren beherrscht: klick
Die Wikipedia hat eine Seite zu Sitzzuteilungsverfahren mit noch mehr Theorie: klick
Update: Mehr zum Thema gibt es bei Fabian Rump, der ein bisschen auf die behauptete Verfassungswidrigkeit eingeht.
- Die genauen Bezeichnungen entnehmen Sie bitte Ihrer Satzung, Paragraph 12 Absatz 2. ↩
- Die Piraten-HSG (!) hat meines Wissens immer noch keine Homepage, auf der man so etwas publizieren könnte. Realsatire pur. ↩
- Kecke These, wo ich doch noch kein Gegenbeispiel für 21 und 33 Plätze gefunden habe. Aber ihr macht das schon. ↩
- Jaa, wenn man im Wahlausschuss sitzt, darf man nicht mehr kandidieren. Deswegen gibt’s da so wenig Personal. Ich will hier nur ein bisschen trollen, lasst mich doch. ↩
- meinetwegen auch ein vom Bundesverfassungsgericht gegebenes Recht ↩